La Géométrie dans l'épreuve de mathématiques du brevet des collèges est souvent redoutée par les élèves en raison de sa complexité et de la diversité des sujets abordés. Parmi les différentes sections des mathématiques, la géométrie occupe une place centrale. Maîtriser les concepts de géométrie est essentiel pour réussir cette épreuve. Cet article vous guidera à travers les théorèmes fondamentaux, les propriétés des figures géométriques, et les formules de calcul d'aires et de volumes. Nous vous fournirons également des exercices types issus des annales du brevet, des astuces pour réussir, et des conseils pour un soutien scolaire efficace.
La géométrie au brevet des collèges couvre plusieurs domaines essentiels : les théorèmes de Thalès et de Pythagore, les triangles semblables et égaux, les propriétés des angles, et les formules de calcul d'aires et de volumes. Ces notions sont cruciales pour résoudre les exercices de géométrie et pour comprendre les démonstrations demandées lors de l'épreuve.
Le théorème de Thalès est un outil puissant pour résoudre des problèmes de proportionnalité et de similitude. Il stipule que si deux droites parallèles coupent deux autres droites sécantes, alors les segments déterminés sur l'une des sécantes sont proportionnels aux segments correspondants sur l'autre sécante.
Énoncé du théorème de Thalès : Si (d1) et (d2) sont deux droites sécantes en un point A, et si (d3) et (d4) sont deux droites parallèles coupant (d1) et (d2) en B et C respectivement, alors :
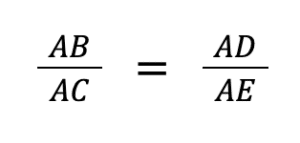
Application pratique :
Prenons un exemple simple pour illustrer l'application du théorème de Thalès. Supposons que nous avons deux droites parallèles coupées par deux autres droites sécantes. Nous devons démontrer que les segments créés sont proportionnels.
Exercice type :
Soient AB = 6 cm, AC = 9 cm, et AD = 4 cm. Trouvez la longueur de AE.
Corrigé :
En utilisant le théorème de Thalès, nous avons :
Le théorème de Pythagore est fondamental pour résoudre des problèmes impliquant des triangles rectangles. Il établit une relation entre les longueurs des côtés d'un triangle rectangle.
Énoncé du théorème de Pythagore :
Dans un triangle rectangle, le carré de la longueur de l'hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés.
où c représente l'hypoténuse, et aa et bb représentent les deux autres côtés.
Application pratique :
Utilisons le théorème de Pythagore pour trouver la longueur de l'hypoténuse d'un triangle rectangle.
Exercice type :
Soient a = 3 cm et b = 4 cm. Trouvez la longueur de l'hypoténuse c.
Corrigé : En utilisant le théorème de Pythagore, nous avons :
La réciproque du théorème de Thalès permet de démontrer que deux droites sont parallèles en utilisant des rapports de proportionnalité.
Énoncé de la réciproque du théorème de Thalès :
Si deux droites sécantes en un point A coupent deux autres droites en B et C respectivement, et si :
alors les droites (DE) et (BC) sont parallèles.
Application pratique :
Démontrons que deux droites sont parallèles en utilisant la réciproque du théorème de Thalès.
Exercice type :
Soient AB = 8 cm, AC = 12 cm, AD = 6 cm, et AE = 9 cm. Démontrez que (DE) et (BC) sont parallèles.
Corrigé :
En utilisant la réciproque du théorème de Thalès, nous avons :
Puisque les rapports sont égaux, les droites (DE) et (BC) sont parallèles.
La réciproque du théorème de Pythagore permet de démontrer qu'un triangle est rectangle en utilisant les longueurs de ses côtés.
Énoncé de la réciproque du théorème de Pythagore :
Si dans un triangle, le carré de la longueur d'un côté est égal à la somme des carrés des longueurs des deux autres côtés, alors le triangle est rectangle.
Application pratique :
Démontrons qu'un triangle est rectangle en utilisant la réciproque du théorème de Pythagore.
Exercice type :
Soient a = 5 cm, b = 12 cm, et c = 13 cm. Démontrez que le triangle est rectangle.
Corrigé :
En utilisant la réciproque du théorème de Pythagore, nous avons :
Puisque a²+ b² = c², le triangle est rectangle.
Les triangles semblables et égaux sont des concepts fondamentaux en géométrie. Comprendre ces notions permet de résoudre de nombreux problèmes impliquant des triangles.
Deux triangles sont semblables s'ils ont les mêmes angles et si les longueurs de leurs côtés correspondants sont proportionnelles.
Application pratique :
Démontrons que deux triangles sont semblables en utilisant les critères de similitude.
Exercice type :
Soient deux triangles ABC et DEF avec AB = 6 cm, AC = 8 cm, BC = 10 cm, DE = 9 cm, DF = 12 cm, et EF = 15 cm. Démontrez que les triangles sont semblables.
Corrigé :
En utilisant les critères de similitude, nous avons :
Puisque les rapports sont égaux, les triangles ABC et DEF sont semblables.
Deux triangles sont égaux s'ils ont les mêmes longueurs de côtés et les mêmes angles.
Application pratique : Démontrons que deux triangles sont égaux en utilisant les critères d'égalité.
Exercice type : Soient deux triangles ABC et DEF avec AB = 6 cm, AC = 8 cm, BC = 10 cm, DE = 6 cm, DF = 8 cm, et EF = 10 cm. Démontrez que les triangles sont égaux.
Corrigé : En utilisant les critères d'égalité, nous avons :
Puisque les longueurs des côtés correspondants sont égales, les triangles ABC et DEF sont égaux.
Les propriétés des angles sont essentielles pour résoudre de nombreux problèmes de géométrie. Comprendre les angles alternes-internes, les droites perpendiculaires et parallèles, et les autres propriétés des angles permet de mieux appréhender les exercices de géométrie.
Les angles alternes-internes sont formés par deux droites coupées par une transversale. Si les deux droites sont parallèles, alors les angles alternes-internes sont égaux.
Application pratique :
Démontrons que deux droites sont parallèles en utilisant les angles alternes-internes.
Exercice type :
Soient deux droites d1 et d2 coupées par une transversale t. Si les angles alternes-internes sont égaux, démontrez que d1 et d2 sont parallèles.
Corrigé :
En utilisant les propriétés des angles alternes-internes, nous avons : Si les angles alternes-internes sont égaux, alors les droites d1 et d2 sont parallèles.
Les droites perpendiculaires et parallèles sont des concepts fondamentaux en géométrie. Comprendre ces notions permet de résoudre de nombreux problèmes impliquant des figures géométriques.
Application pratique :
Démontrons que deux droites sont perpendiculaires en utilisant les propriétés des angles.
Exercice type :
Soient deux droites d1 et d2 qui se coupent en formant un angle de 90°. Démontrez que d1 et d2 sont perpendiculaires.
Corrigé :
En utilisant les propriétés des angles, nous avons :
Si l'angle formé par deux droites est de 90°, alors les droites sont perpendiculaires.
Les formules de calcul d'aires et de volumes sont essentielles pour résoudre des problèmes de géométrie impliquant des figures planes et des solides.
Formules :
Exercice type :
Calculez le périmètre et l'aire d'un carré de côté a = 5 cm.
Corrigé :
Formules :
Exercice type :
Calculez le périmètre et l'aire d'un rectangle de longueur l = 6 cm et de largeur L = 4 cm.
Corrigé :
Formules :
Exercice type :
Calculez le périmètre et l'aire d'un triangle de base b = 8 cm et de hauteur h = 5 cm.
Corrigé :
Formules :
Exercice type :
Calculez le périmètre et l'aire d'un cercle de rayon r = 3 cm.
Corrigé :
Formule :
Exercice type :
Calculez le volume d'un cube de côté a = 4 cm.
Corrigé :
Formule :
Exercice type :
Calculez le volume d'un cylindre de rayon r = 2 cm et de hauteur h = 6 cm.
Corrigé :
Formule :
Exercice type :
Calculez le volume d'une pyramide à base carrée de côté a = 5 cm et de hauteur h = 8 cm.
Corrigé :
Formule :
Exercice type : Calculez le volume d'un cône de rayon r = 3 cm et de hauteur h = 7 cm.
Corrigé :
Formule :
Exercice type :
Calculez le volume d'une sphère de rayon r = 4 cm.
Corrigé :
Pour vous entraîner efficacement, il est essentiel de pratiquer avec des exercices issus des annales du brevet. Voici quelques exemples d'exercices types et leurs corrigés.
Énoncé : Soient deux droites parallèles (d1) et (d2) coupées par deux autres droites sécantes en A, B, C, et D respectivement. Si AB = 7 cm, AC = 10 cm, et AD = 5 cm, trouvez la longueur de AE.
Corrigé :
En utilisant le théorème de Thalès, nous avons :
Énoncé :
Soient a = 6 cm et b = 8 cm. Trouvez la longueur de l'hypoténuse c.
Corrigé :
En utilisant le théorème de Pythagore, nous avons :
Énoncé : Soient AB = 9 cm, AC = 12 cm, AD = 8 cm, et AE = 10 cm. Démontrez que (DE) et (BC) sont parallèles.
Corrigé :
En utilisant la réciproque du théorème de Thalès, nous avons :
Puisque les rapports ne sont pas égaux, les droites (DE) et (BC) ne sont pas parallèles.
Énoncé :
Soient a = 7 cm, b = 24 cm, et c = 25 cm. Démontrez que le triangle est rectangle.
Corrigé :
En utilisant la réciproque du théorème de Pythagore, nous avons :
Puisque a²+ b² = c², le triangle est rectangle.
Le soutien scolaire à domicile est une excellente solution pour aider votre enfant à réussir son brevet des collèges. Voici quelques avantages et conseils pour choisir un bon professeur particulier.
La géométrie est une partie essentielle du programme de mathématiques du brevet des collèges. En maîtrisant les théorèmes fondamentaux, les propriétés des figures géométriques, et les formules de calcul d'aires et de volumes, votre enfant sera bien préparé pour réussir cette épreuve. N'hésitez pas à utiliser les annales du brevet pour vous entraîner et à faire appel à un soutien scolaire à domicile pour un accompagnement personnalisé. Avec de la pratique et de la persévérance, votre enfant pourra aborder le brevet des collèges avec confiance et sérénité.
Chez Didasko, nous sommes spécialistes du soutien scolaire à domicile sur la région toulousaine. Déclaré Service à la Personne, nous faisons bénéficier à nos clients du service d'Avance Immédiate.
Réservez votre cours d'essai offert avec Didasko
Pour approfondir vos connaissances et vous entraîner davantage, consultez les ressources suivantes :